二叉查找树(BST)特性:
- 左子树上所有节点的值均小于等于它的根节点的值
- 右子树上所有节点的值均大于等于它的根节点的值
- 左,右子树也分别为二叉查找树
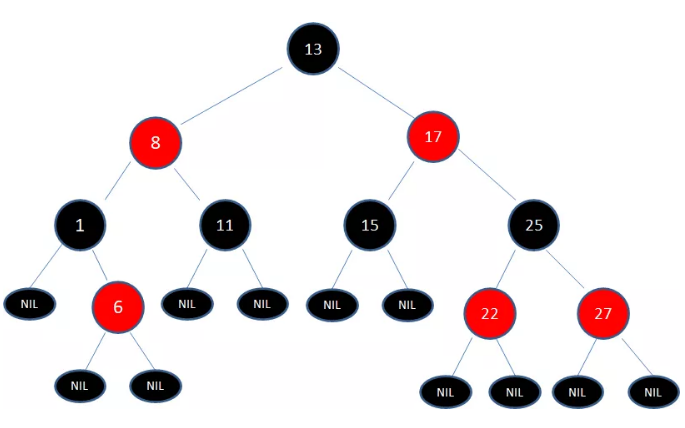
红黑树(Red Black Tree)是一种自平衡的二叉查找树,除了符合二叉查找树的基本特性外,它还具有下列附加特性:
- 节点是红色或黑色
- 根节点是黑色
- 每个叶子节点都是黑色的空节点(NIL节点)
- 每个红色节点的两个子节点都是黑色节点(从每个叶子到根的所有路径上不能有两个连续的红色节点)
- 从任一节点到其每个叶子节点的所有路径均包含相同数目的黑色节点
变色:把红色节点变为黑色,或者把黑色节点变为红色。
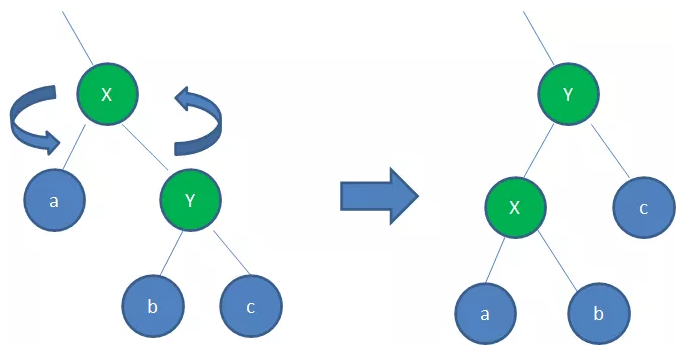
左旋转:逆时针旋转红黑树的两个节点,使得父节点被自己的右孩子取代,而自己成为自己的左孩子。
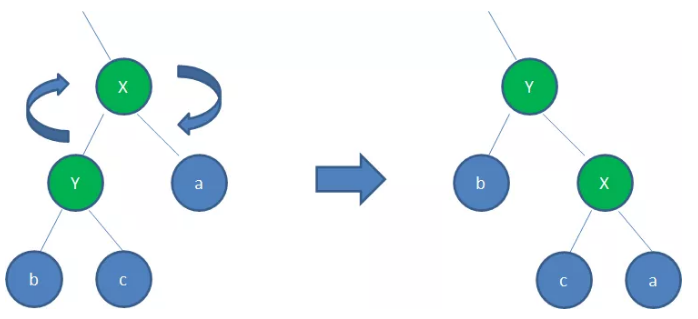
右旋转:顺时针旋转红黑树的两个节点,使得父节点被自己的左孩子取代,而自己成为自己的右孩子。
红黑树的插入:
局面1:新节点(A)位于树根,没有父节点。
直接让新节点变色为黑色即可。
局面2:新节点(B)的父节点为黑色。
不需要任何调整。
局面3:新节点(D)的父节点和叔叔节点都是红色。
从父节点-祖父节点-叔叔节点,由原来的红-黑-红变色为黑-红-黑。
局面4:新节点(D)父节点是红色,叔叔节点是黑色或者没有叔叔节点。
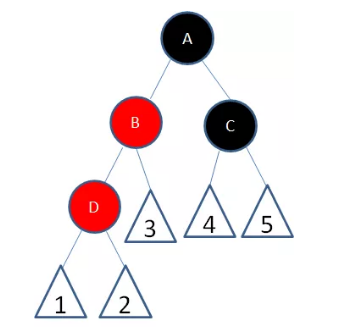
此时要区分情况,新节点是父节点的左孩子或者右孩子,父节点是祖父节点的左孩子或者右孩子。如果父节点是祖父节点的左孩子,则将新节点调整为父节点的左孩子;如果父节点是祖父节点的右孩子,则将新节点调整为父节点的右孩子。
先按照上述规则旋转新节点为父节点对应位置的孩子,然后将父节点旋转到原来祖父节点的位置,接着让父节点变色为黑色,原来的祖父节点变色为红色。
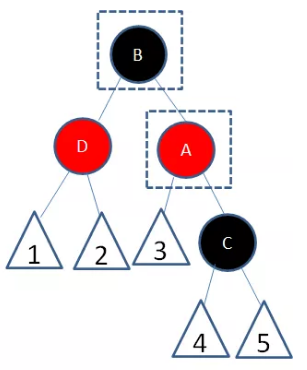
红黑树的删除:

